 |
 |
|
 |
Содержание |
224
Для дальнейшего анализа воспользуемся системой индексов переменного состава
(
ПС
i1
i0
i1
i1
i0
i0
I
З
З
З
d
З
d
*
*
), фиксированного состава (
ФС
i1
i1
i0
i1
I
З
d
З
d
*
*
) и влияния структурным
сдвигов (
СТР
i0
i1
i0
i1
I
З
d
З
d
*
*
).
Расчет индексов представим в таблице 12.2 (с использованием таблице 12.1).
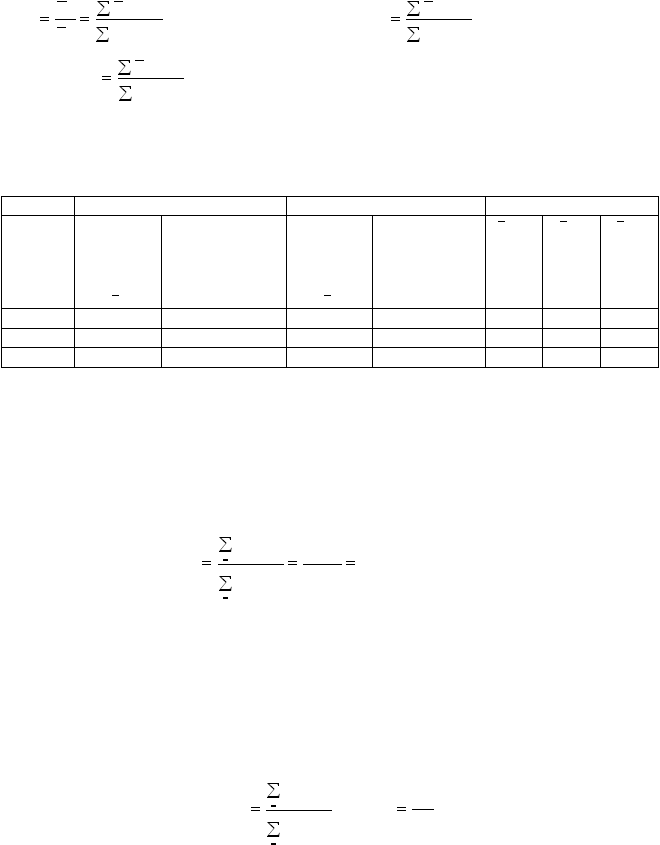
Таблица 12.2
Расчет индексов затрат на изготовление образцов
Базовый период
Текущий период
Расчетные показатели
Образц
ы
Средние
затраты
на один
образец,
i0
З
Доля
изготовленным
образцов в
общем числе,
ni0
d
Средние
затраты
на один
образец,
i1
З
Доля
изготовленны
м образцов в
общем числе,
i1
d
i0
n0
З
d
i1
З
d
1
i0
З
d
1
1
1613
0,6
1755
0,8
968
1404
1290
2
3080
0,4
3780
0,2
1232
756
616
Итого
2200
1,0
2160
1,0
2200
2160
1906
Нетрудно убедится, что итог группы 1 и 3 соответствует итогу групп 5 и 6, то есть
результат расчета индекса переменного состава с разложением на внутрипроизводственные и
структурные факторы совпадает с расчетом по выше приведенной методике.
Индекс фиксированного
состава покажет влияние изменения затрат по отдельным
образцам на изменение общим средним затрат:
ФС
i1
i1
i
n
i0
i1
i
n
I
З
d
З
d
1
1
2160
1906
1133
*
*
,
или 113,3%.
Изменение затрат на изготовление одного образца при им структуре на уровне
отчетного периода могло бы привести к повышению общим средним затрат на 254 тыс. руб.
Однако, в текущем периоде снизилась доля образцов с более высокими затратами на
изготовление одного образца.
Изменение структуры числа изготовленным образцов следующим образом повлияло
на изменение общим средним затрат:
СТР
i0
i1
i
n
i0
i1
i
n
I
З
d
З
d
1
1
*
*
или
СТР
ПС
ФС
I
I
I
.
В нашем примере:
