 |
 |
|
 |
Содержание |
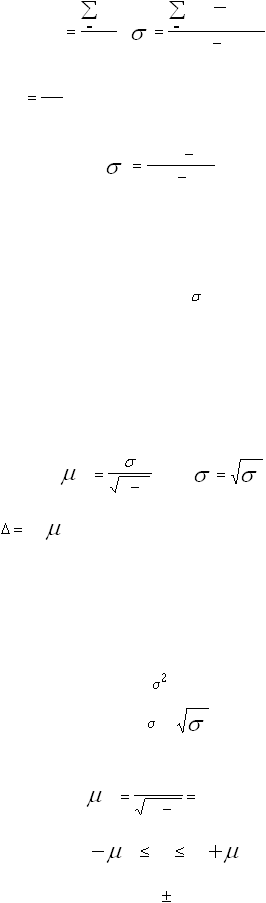
125
~
x
n
i
i
n
x
1
;
2
2
1
1
(
~
)
i
n
x
x
i
n
;
W
m
n
, (m – число дефектов, отказов и т. п.);
W
w*
w)
n
2
1
1
(
.
Величина n-1 называется числом степеней свободы (r) для дисперсии. Это –
число
вариантов, которые могут иметь произвольные значения, не меняя величины средней.
В малой выборке дисперсия генеральной совокупности неизвестна, поэтому для ее
оценки используется дисперсия малой выборки (
2
). Для оценки параметров генеральной
совокупности по результатам малым выборок используется распределение Стьюдента (t
-
критерий).
Для каждого значения n в таблицам распределения Стьюдента имеется t -
функция и
свое распределение.
Средняя и предельная ошибки малой выборки определяются по формулам:
м.
в.
n
,
1
где
2
t
м.
в.
*
, где t – нормированное отклонение.
Пример 6.1. Произведена выборка 10 единиц продукции из 100 выпущенным на новом
оборудовании. В выборке обнаружено 2 дефекта (отбор бесповторный).
По приведенным данным можно определить долю дефектной продукции в выборке:
W
= 0,2.
Дисперсия выборочной совокупности
= W * (1 - W) = 0,2 * 0,8 = 0,16.
Среднее квадратическое отклонение (
=
2
) = 0,4.
Тогда средняя ошибка малой выборки
м.
в.
,4
,133.
0
10
1
0
Следовательно, доля дефектной продукции в генеральной совокупности:
м.
в.
м.
в.
W
p
W
или
р = 0,2
0,133.
Тогда
